Winding Speed Calculation and Package Density Measurements

Many of us know the famous quote “well-wound is half dyed,” which stands to be true to this day. Any imperfection left in the soft wound package can result in dire consequences that are not rectifiable. Thus, it’s of utmost importance that we maintain each winding parameter perfectly by careful and accurate measurements.

Also, to be wary of the production we need to be well-informed about the winding speed calculation.

Winding Speed Calculation

Now, the winding or production speed of a particular spindle depends on various factors. Among them, the surface speed and count seems to be the most important factors.

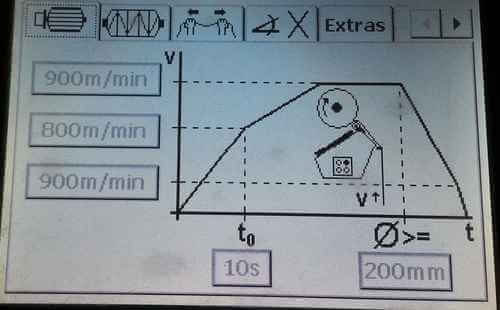
Setting the Surface Speed of the Package

Let’s check out the formula for soft winding speed calculation for cotton –

Say,

Bobbin’s Surface Speed = 900 m/min

Total No. of Spindle = 990

Efficiency = 85% (assumed)

Count = 40/1 Ne (assumed)

Winding Production Speed = {(Bobbin’s Surface Speed ×No.of Spindle ×60 ×24 ×Efficiency ×1.09) ÷ (840 ×Count ×2.2046)} kg/day

= {(900 ×990 ×60 ×24 ×0.85 ×1.09) ÷ (840 ×40 ×2.2046)} kg/day

= 16,047.84 kg/day

= 16.05 ton/day

For calculating winding production of filaments in the denier count system, you can use the following formula to convert it to Ne or insert the value directly into the equation –

Ne = 5315 ÷ den

What is Package Density

It’s the weight of the wound yarn per its volume. This factor is crucial to ensure that the yarn/filament package meets our machine’s requirements.

Too higher density will result in a package that will hinder the uniform flow of dye liquor. And too lower density will culminate in the yarns coming out of the package due to the differential pressure of the dyeing machine.

How to Calculate Package Density After Soft Winding

The package density is calculated by the following equations –

Say,

Empty bobbin diameter, d = 6.4 cm

Full bobbin diameter, D = 15.5 cm

Traverse length, h = 15 cm

Weight of yarn in the package, M = 900 gm

Volume of yarn in the package, V = {(ΠD²h÷4) − (Πd²h÷4)} cm³

= {(Πh÷4) × (D² − d²)} cm³

= [{(3.1416 × 15) ÷4} × (15.5² − 6.4²)] cm³

=2347.83 cm³

Package Density =  Weight of Yarn in the Package (M) ÷ Volume of Yarn in the Package (V)

= 900 ÷ 2347.83 gm/cm³

= 0.38 gm/cm³

Generally, Package Density of 0.35 – 0.38 gm/cm³ is Preferable.

What is Layer Density

It’s the same as package density, just different in a way that here we’ll calculate the density of each package layer by layer. This will allow us to ensure that the yarn/filament is distributed uniformly throughout the package. Often times. due to patterning problems, some layers tend to boast higher density, which creates troubles in liquor flow. Thus, it’s crucial to make sure our soft wound package has a uniform density all throughout.

How to Calculate Layer Density of a Soft Wound Package

First, we’ll have to start numbering the layers. You don’t need to mark it on the package. Just keep in mind that whether you’re starting your numbering from the inside or outside.

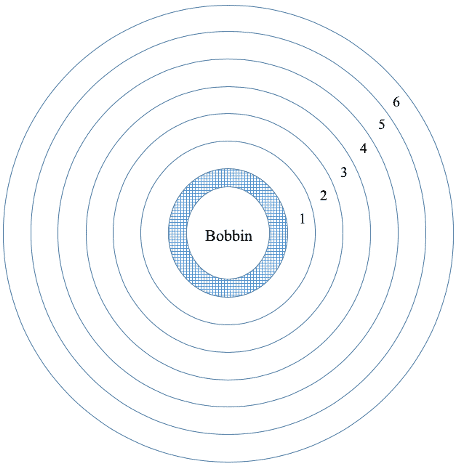
As you can see, we’ve divided the package into six layers. But you can choose to go higher or lower according to your convenience.

Now, we’re going do the following –

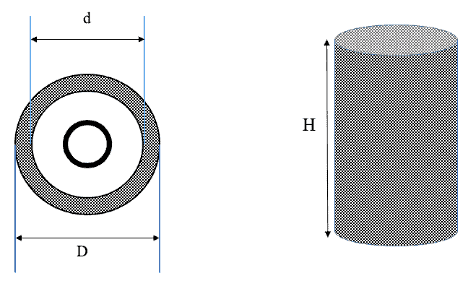
1. The total length of the yarn wound on the package is divided by six.
2. After unwinding each layer bobbin diameter & weight was taken.
3. Calculations are done using the following formula –

Layer Density = Weight of Yarn of Each Layer ÷ Volume of Yarn of Each Layer

= {(Weight Before Unwinding − Weight After Unwinding) ÷ (Volume Before Unwinding-Volume After Unwinding)}

= {4×(M₁ − M₂)} ÷ {ΠH(D² − d²)}

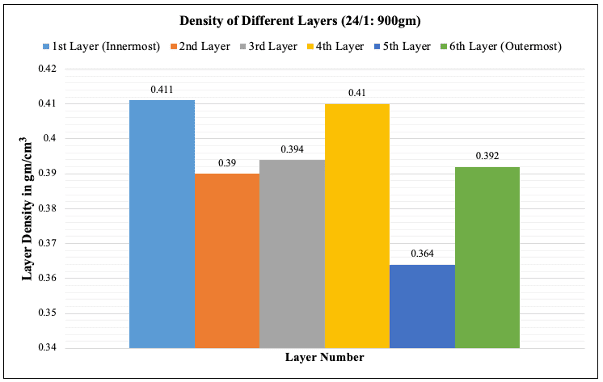
Layer No.	Initial Dia	Final Dia	Initial Weight	Final Weight	Difference	Traverse	Density
6	15.3	14.2	893	742	151	15.1	0.392
5	14.2	12.9	742	590	152	15.1	0.364
4	12.9	11.6	590	435	155	15.1	0.410
3	11.6	10.1	435	283	152	15.1	0.394
2	10.1	8.3	283	130	153	15.1	0.390
1	8.3	6.5	130	0	130	15.1	0.411

Sample Data of Layer Density

Layer No.	Initial Dia	Final Dia	Initial Weight	Final Weight	Difference	Traverse	Density
6	15.3	14.2	893	742	151	15.1	0.392
5	14.2	12.9	742	590	152	15.1	0.364
4	12.9	11.6	590	435	155	15.1	0.410
3	11.6	10.1	435	283	152	15.1	0.394
2	10.1	8.3	283	130	153	15.1	0.390
1	8.3	6.5	130	0	130	15.1	0.411

Calculation of Wound Yarn Length

The amount of yarn that needs to be wound on the package has to be calculated first, depending on the required weight of a yarn in the package because the yarn winding machines take the yarn length as input, not the weight. It’s calculated by the following formula –

Length in Meters = Count (Ne) × Weight of Yarn (gm) × 1.69

For Filaments with Denier Count (Direct Count System)

Length for Meters = (Weight of Yarn in gm × 9000) ÷  Count in Denier

Frequently Asked Questions

1. Why do we need surface speed of the bobbin for calculating production?

The surface speed refers to how much yarn is wound per minute. You see, the package diameter increases as time goes by. As a result, the package will take up more yarn per revolution than it took when it started if the RPM is kept constant. That’s why the surface speed is taken into account. The machine adjusts the RPM according to the surface speed.

For example, if you set the surface speed to 100 m/min, then initially, the spindle will rotate more to wind 100 meters per minute. But as the package builds up and the diameter increases, it’ll rotate less time to wind that same amount of yarn. This is done with the help of servo motors.

2. Why can’t we directly input weight instead of length?

That’s because the weight can change according to the moisture content. For spun yarn types, like cotton, the weight variation due to the humidity fluctuations is pretty significant. So, if the quantity of material wound would not be constant, resulting in numerous problems.

By now, I hope you’ve grasped all the concepts regarding winding speed calculation and measuring the package densities and other aspects.

REFERENCES

1. Cross Winding of Yarn Packages
2. Suitable Traverse Ratios for Step Precision Winding
3. Textile Sizing – Bhuvenesh C. Goswami, ‎Rajesh D. Anandjiwala, ‎David Hall